[개발자를 위한 LLM] 트랜스포머 셀프 어텐션 상세 동작 과정 (Transformer Self Attention Detailed Process)

"이 포스팅은 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다."

By KJJ88

IT/Large Language Model

2024. 4. 16. 19:38

이전 포스팅까지는 트랜스포머의 셀프 어텐션과 멀티 헤드 어텐션에 대해서 알아봤고,

이번 포스팅에서는 셀프 어텐션의 상세한 동작 과정에 대해서 알아보겠습니다.

셀프 어텐션의 계산 과정 (Self Attention in Detail)

셀프 어텐션의 동작 과정을 벡터 계산 과정과 행렬 계산 과정으로 두 번에 걸쳐서 설명하겠습니다.

벡터 계산으로 셀프 어텐션 과정 알아보기 (Self Attention using Vector)

셀프 어텐션을 계산하는 첫 단계는 인코더의 입력 벡터들로부터 각 단어에 대한 세 가지 벡터인 Query, Key, Value를 생성하는 것입니다.

이는 각 단어의 임베딩을 훈련 과정에서 학습한 세 개의 행렬(WQ, WK, WV)에 곱하여 이루어집니다.

예를 들어, x1을 WQ 가중치 행렬로 곱하면 해당 단어에 대한 Query 벡터 q1이 생성됩니다. 이런 방식으로 입력 문장의 각 단어에 대해 Query, Key, Value 투영을 생성합니다. 생성된 이 새로운 벡터들은 원래 임베딩 벡터보다 차원이 작습니다. 이들의 차원은 64인 반면, 원래의 임베딩과 인코더 입력/출력 벡터의 차원은 512입니다.

이렇게 차원을 줄이는 것은 필수적이지 않지만, 다중 헤드 어텐션 계산을 대체로 일정하게 유지하기 위한 아키텍처적 선택입니다.

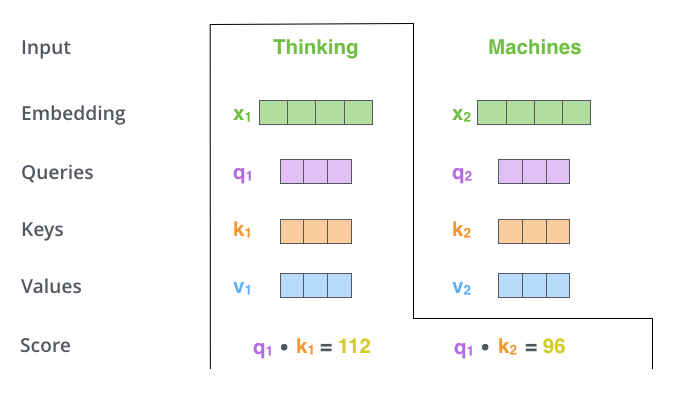
셀프 어텐션을 계산하는 두 번째 단계는 각 단어에 대한 점수를 계산하는 것입니다.

예를 들어, "Thinking"이라는 첫 번째 단어에 대한 셀프 어텐션을 계산한다고 할 때, 이 단어에 대해 입력 문장의 다른 모든 단어를 점수 매깁니다. 이 점수는 입력 문장의 다른 부분에 얼마나 초점을 맞출지를 결정하는 데 사용됩니다.

점수 계산은 Query 벡터와 각 단어의 Key 벡터의 내적을 취함으로써 이루어집니다. 예를 들어, 첫 번째 단어의 경우, 첫 번째 점수는 Query 벡터 q1과 첫 번째 Key 벡터 k1의 내적이 됩니다. 마찬가지로, 두 번째 점수는 q1과 두 번째 Key 벡터 k2의 내적이 됩니다. 이렇게 계산된 점수를 통해 모델은 각 단어가 전체 문장에서 어떤 역할을 하는지, 어떻게 다른 단어들과 상호 작용하는지를 파악할 수 있습니다.

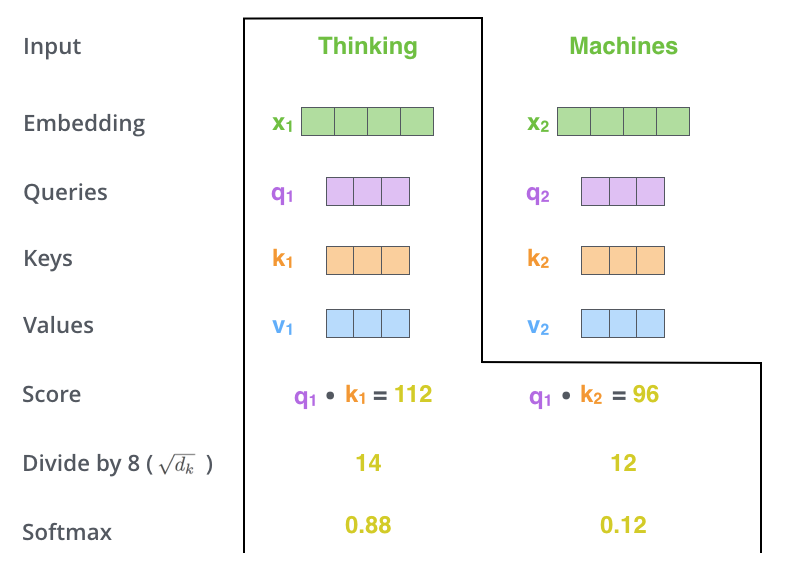
셀프 어텐션 계산의 세 번째와 네 번째 단계에서는 먼저 계산된 점수를 8로 나눕니다. 이는 Key 벡터의 차원인 64의 제곱근에 해당하며, 더 안정적인 기울기를 얻기 위해 사용됩니다. 다른 값들도 사용될 수 있지만, 8은 기본값으로 설정되어 있습니다.

이렇게 조정된 점수는 소프트맥스 연산을 통해 정규화됩니다. 소프트맥스는 점수들을 모두 양수로 변환하고, 이들의 총합이 1이 되도록 만듭니다. 소프트맥스 점수는 각 단어가 특정 위치에서 얼마나 영향력을 가질지를 결정합니다. 일반적으로 해당 위치에 있는 단어가 가장 높은 점수를 받지만, 현재 단어와 관련된 다른 단어에 주의를 기울이는 것이 때로는 유용할 수 있습니다.

이러한 메커니즘을 통해 모델은 문장 내의 각 단어의 중요도와 상호작용을 더 잘 파악하고, 전체 문맥을 고려한 정확한 인코딩을 수행할 수 있습니다.

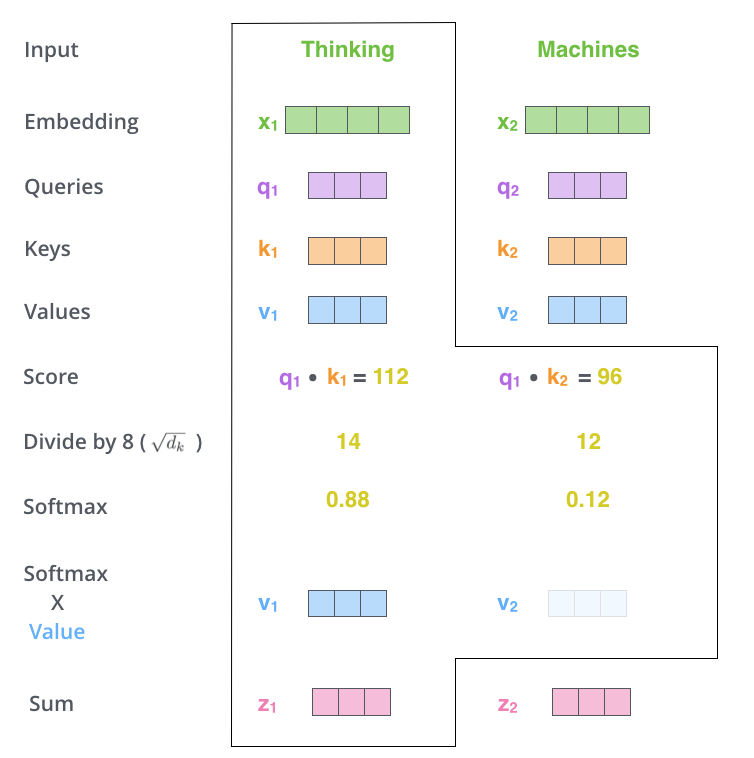
셀프 어텐션 계산의 다섯 번째 단계에서는 각 Value 벡터에 소프트맥스 점수를 곱합니다. 이는 주목하고자 하는 단어들의 값을 유지하고 관련 없는 단어들을 축소하는 데 목적이 있습니다.

여섯 번째 단계에서는 이렇게 가중치가 적용된 Value 벡터들을 합산하여, 해당 위치에서의 셀프 어텐션 레이어의 출력을 생성합니다. 이 출력은 피드 포워드 신경망으로 전달될 벡터입니다.

이상으로 벡터 계산을 통한 셀프 어텐션의 동작 과정을 알아보았습니다. 실제 구현에서는 이러한 계산이 행렬 형태로 수행되어 더 빠르게 처리되기 때문에 행렬 계산을 통한 셀프 어텐션의 동작도 알아보겠습니다.

행렬 계산을 통한 셀프 어텐션 동작 과정 (Self Attention using Matrix)

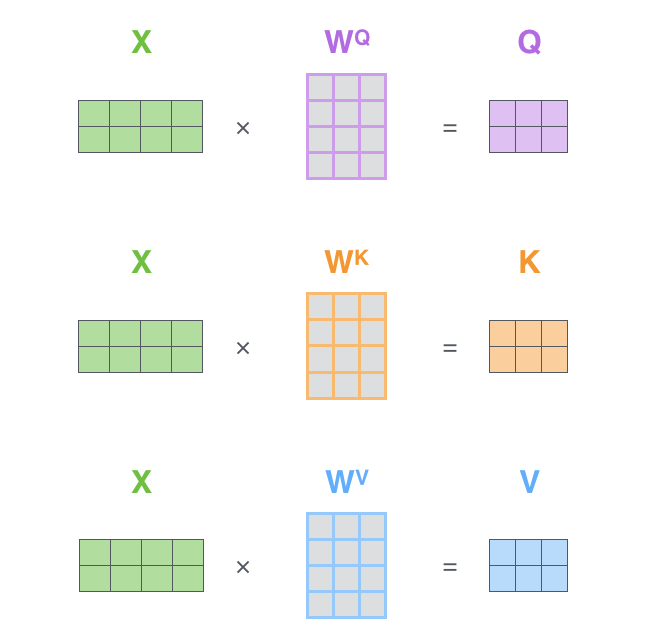
행렬을 이용한 셀프 어텐션 계산의 첫 단계는 Query, Key, Value 행렬을 만드는 것입니다.

이를 위해 우리는 임베딩을 행렬 X로 구성하고, 훈련된 가중치 행렬 WQ, WK, WV와 곱합니다. X 행렬의 각 행은 입력 문장의 각 단어를 나타냅니다. 임베딩 벡터는 512차원이고, q/k/v 벡터는 64차원으로 크기가 다릅니다.

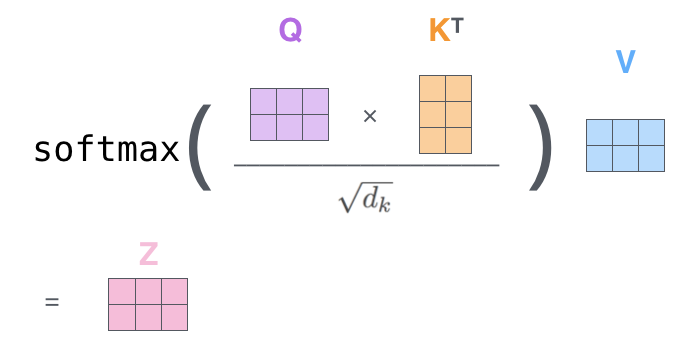
행렬을 사용하는 덕분에, 셀프 어텐션 레이어의 출력을 계산하는 데 필요한 두 번째 단계부터 여섯 번째 단계까지의 과정을 하나의 공식으로 요약할 수 있습니다. 이렇게 하면 셀프 어텐션 계산을 훨씬 효율적으로 처리할 수 있습니다.

셀프 어텐션 계산을 파이토치 코드로 구현해봤습니다.

import torch
import numpy as np
from torch.nn.functional import softmax

x = torch.tensor([
    [1.0, 0.0, 1.0, 0.0],
    [0.0, 2.0, 0.0, 2.0],
    [1.0, 1.0, 1.0, 1.0],
])
w_query = torch.tensor([
    [1.0, 0.0, 1.0],
    [1.0, 0.0, 0.0],
    [0.0, 0.0, 1.0],
    [0.0, 1.0, 1.0]
])
w_key = torch.tensor([
    [0.0, 0.0, 1.0],
    [1.0, 1.0, 0.0],
    [0.0, 1.0, 0.0],
    [1.0, 1.0, 0.0]
])
w_value = torch.tensor([
    [0.0, 2.0, 0.0],
    [0.0, 3.0, 0.0],
    [1.0, 0.0, 3.0],
    [1.0, 1.0, 0.0]
])

querys = torch.matmul(x, w_query)
keys = torch.matmul(x, w_key)
values = torch.matmul(x,w_value)

attn_scores = torch.matmul(querys, keys.T)
key_dim_sqrt = np.sqrt(keys.shape[-1])
attn_probs = softmax(attn_scores / key_dim_sqrt, dim=1)
weighted_values_Z = torch.matmul(attn_probs, values)